Iterative Methods for the Poisson’s Equation and the New Laplace Solver via Rational Approximations

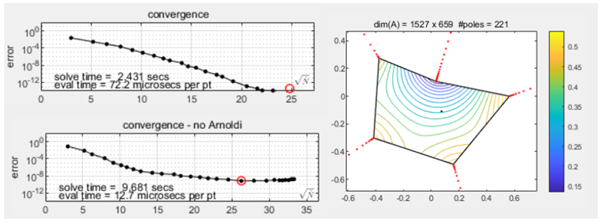
This project explores efficient numerical methods for solving the 2D Poisson’s equation with Dirichlet boundary conditions, a problem with applications in fields such as electromagnetism, fluid dynamics, and quantum mechanics. The equation is discretized using a finite difference scheme, transforming it into a large linear system. Several solution techniques are investigated, including basic iterative methods, multigrid methods, and preconditioned conjugate gradient (CG) methods, with a particular focus on their convergence properties and computational efficiency. Additionally, a novel method based on rational approximations is introduced for solving Laplace’s equation on irregular domains. This new approach, leveraging lightning algorithms and Arnoldi orthogonalization, achieves root-exponential convergence and shows promising results for domains with corner singularities. Numerical results demonstrate the performance of these methods across different problem configurations, with multigrid methods and preconditioned CG emerging as highly effective solvers for large systems.