Dynamics of Neural Network Parameters in Training: Modelling SGD by a Limiting PDE

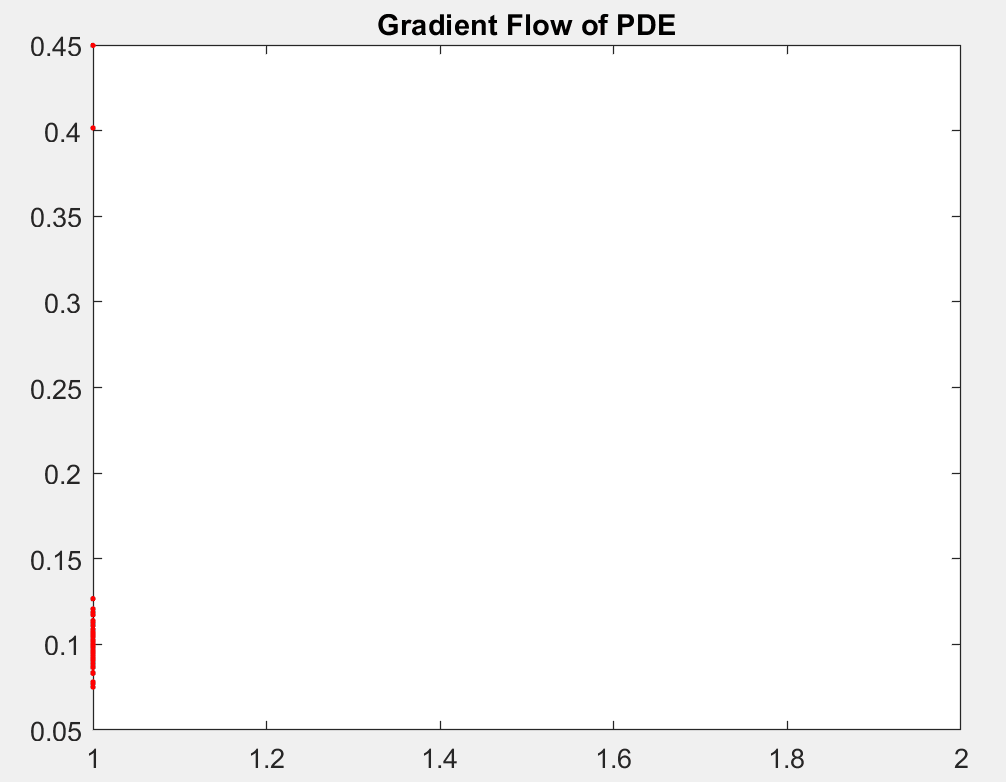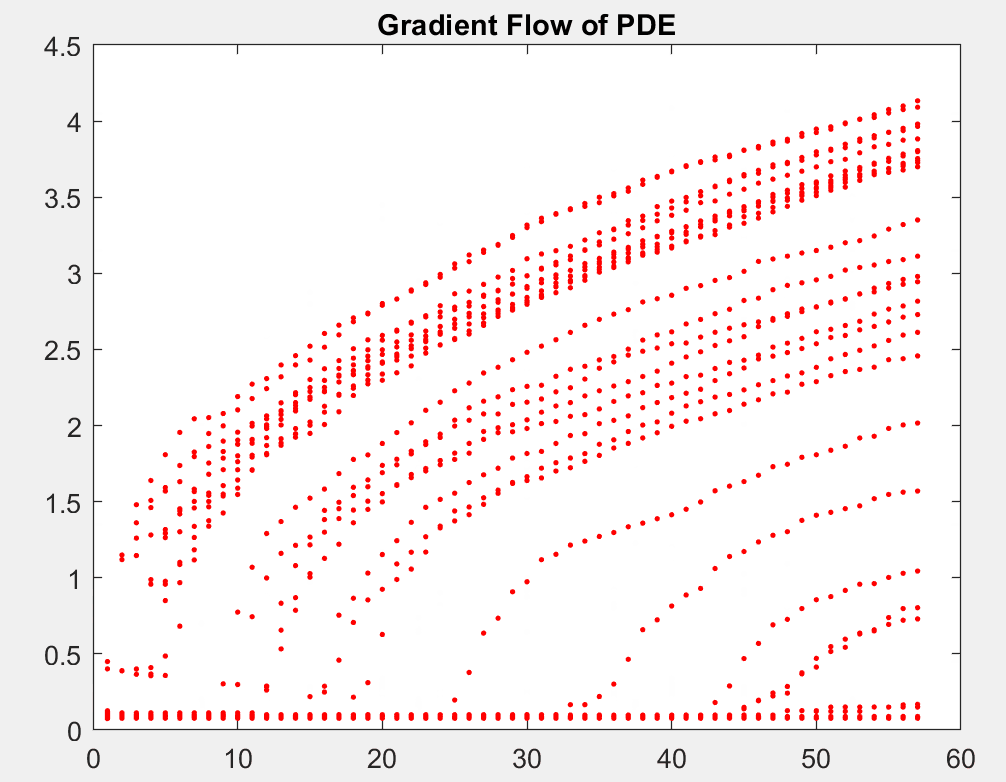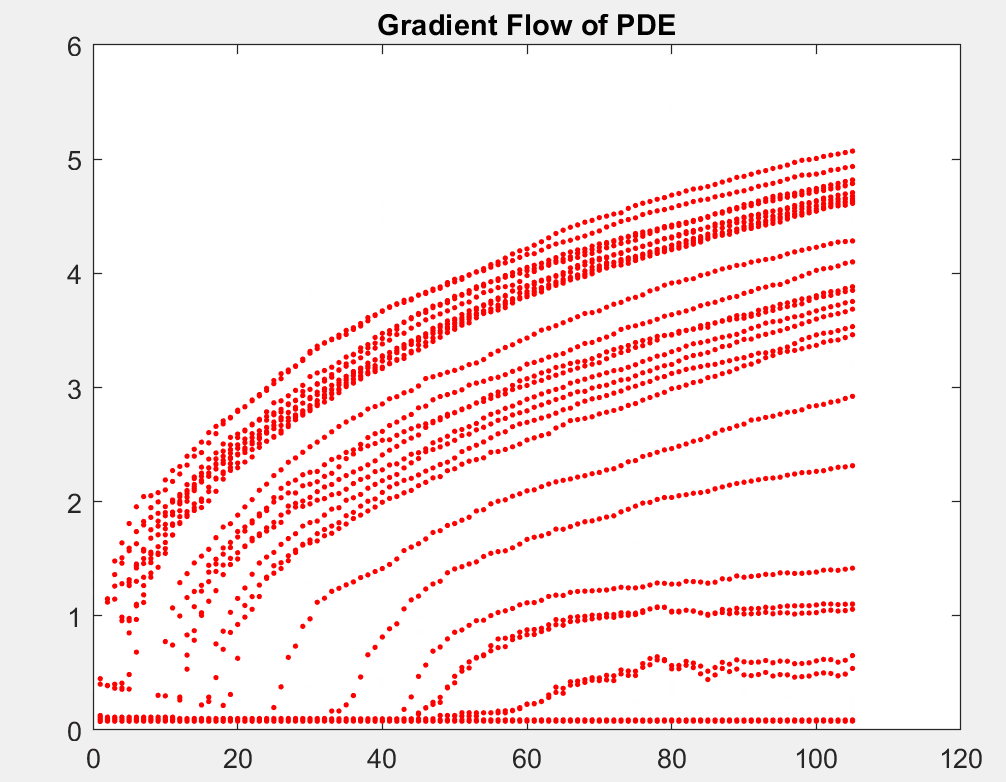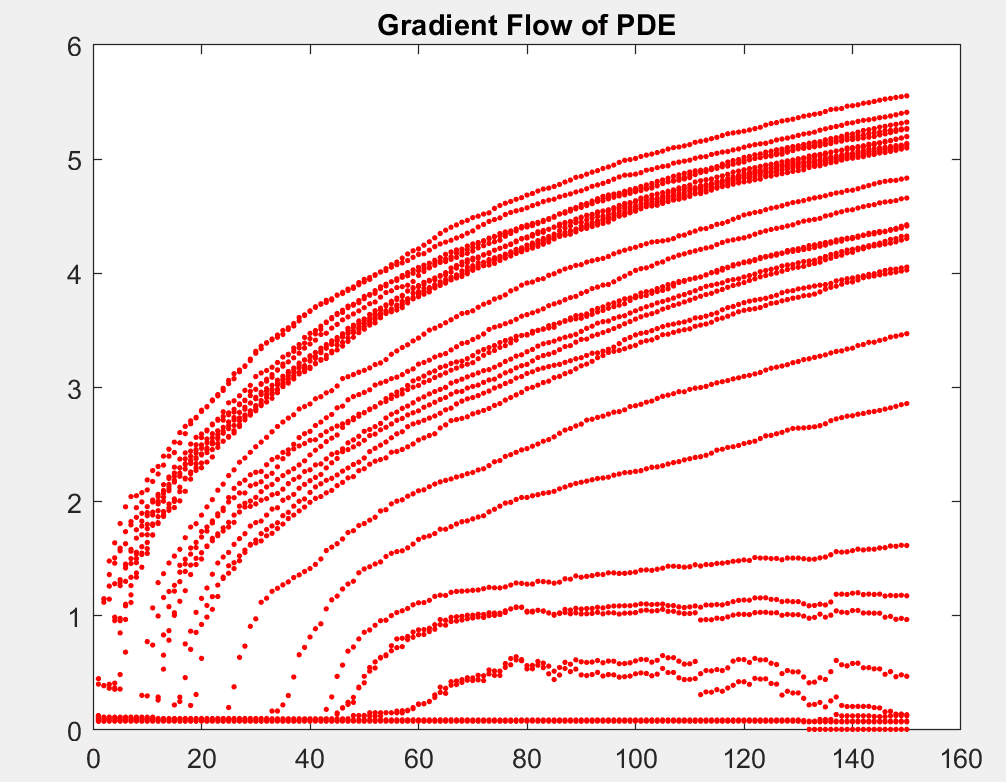
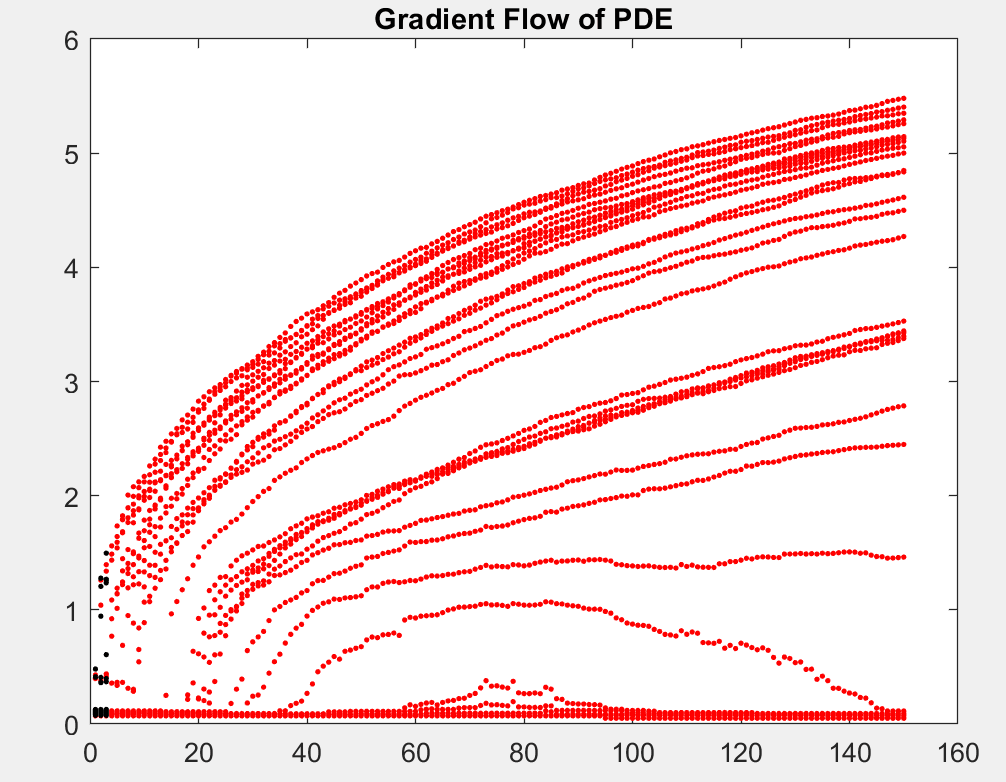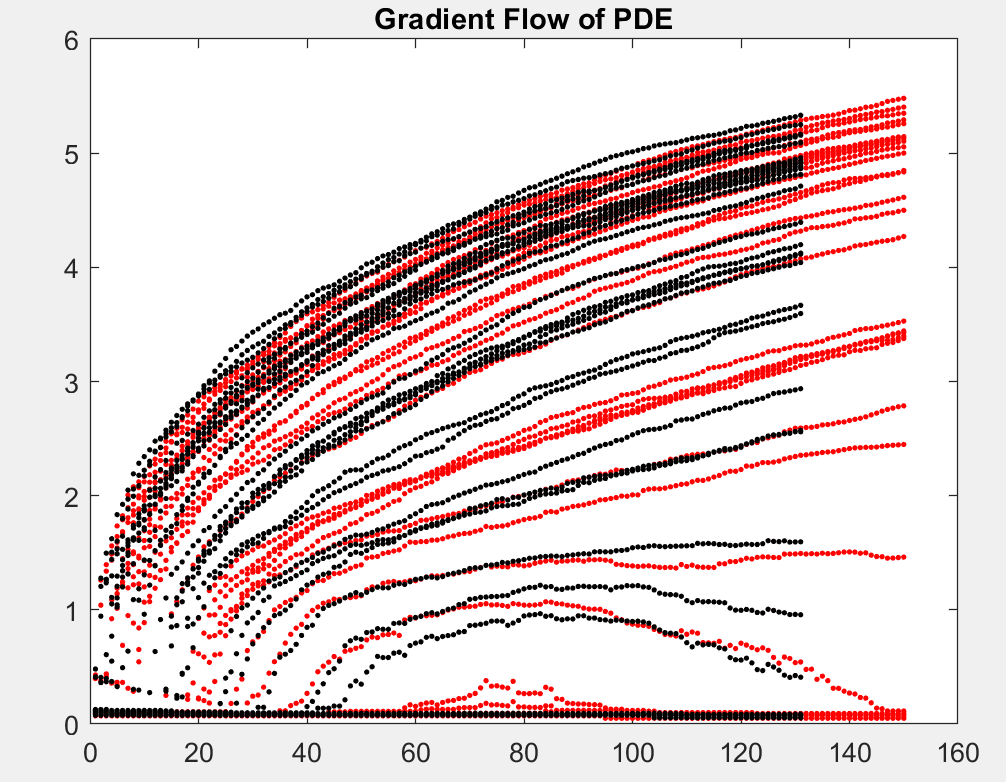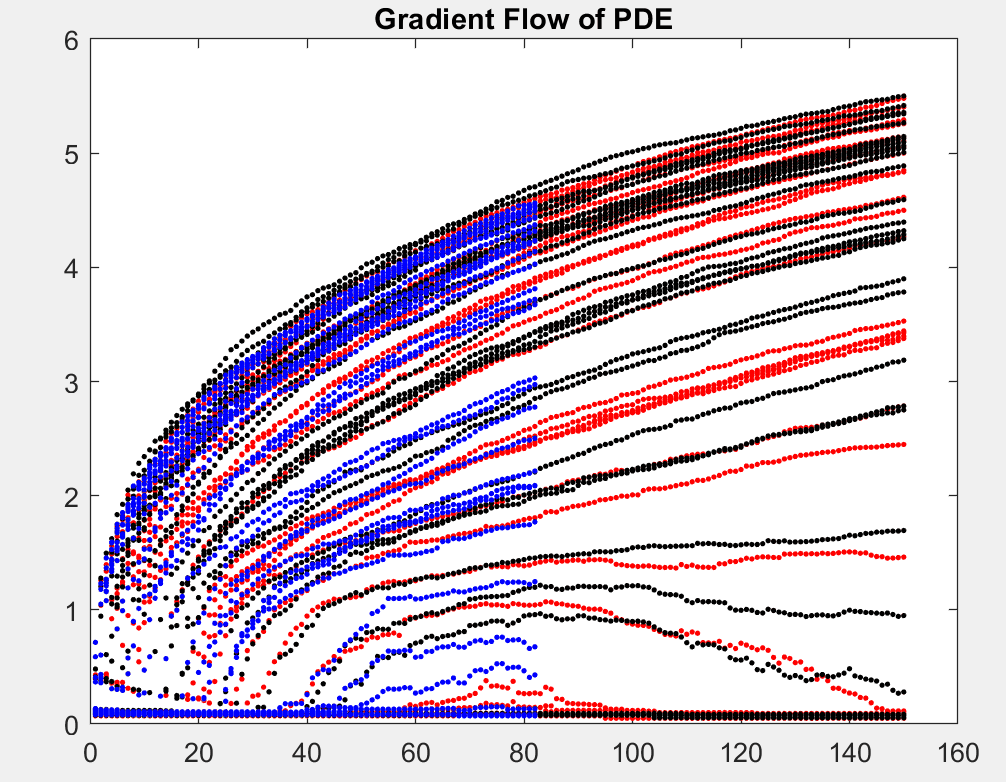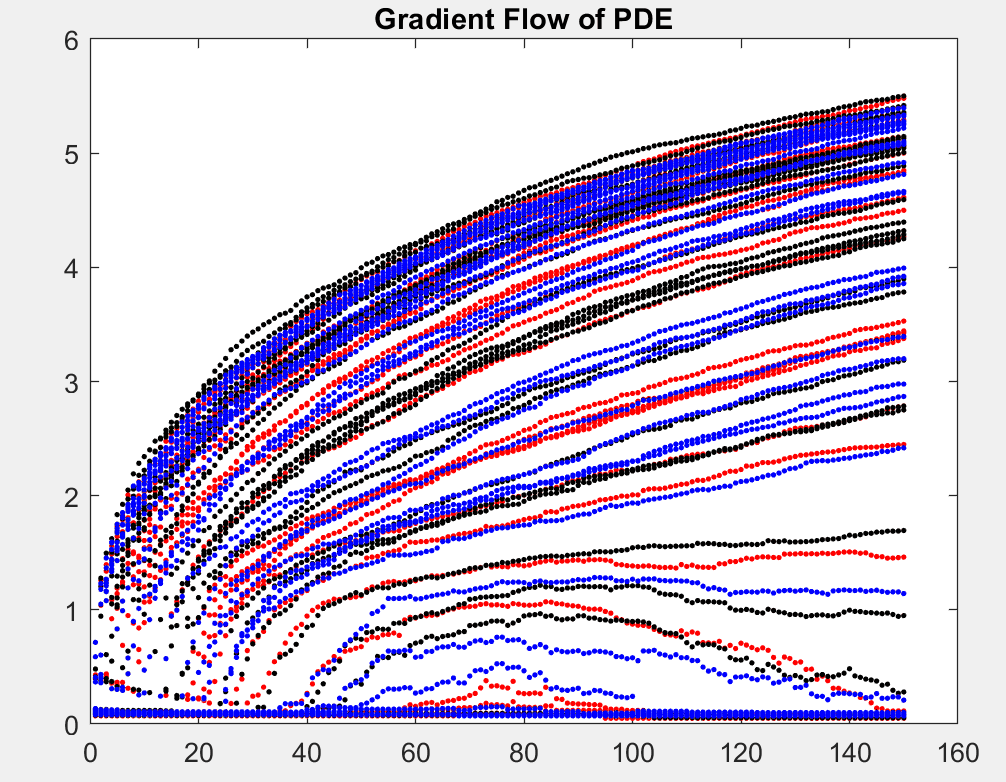
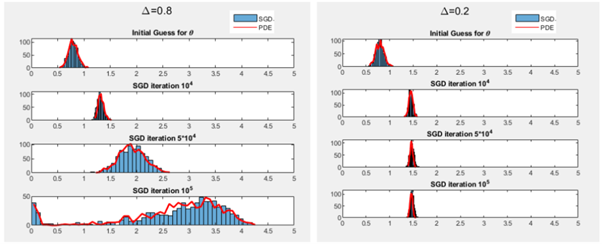
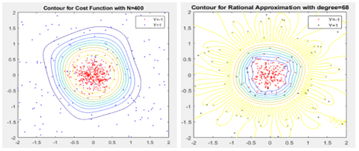
Using stochastic gradient descent (SGD) algorithms to learn data is a complicated high dimensional optimization problem. In this project, we reinterpret SGD as the evolution of a particle system. Such evolution can be modelled by a limiting partial differential equation (PDE). Among multiple numerical examples, we illustrate how this PDE can be used to infer the convergence profile of SGD and why SGD dynamics do not become more complex when the network size increases.